【ベイズ推論_PyMC】モデルの比較 -LOO-

ベイズ推論を行う場合，モデルの形状をある程度指定する必要があります。
そうした場合，作成したモデル間の精度を比較し，どのモデルを採用するかといった作業が必要です。

本記事では，モデル比較の手法としてLOOを使用してみたいと思います。

LOO

今回，詳しい紹介は省きますが，LOO(Leave-one-out-cross-validation)は情報量基準の考え方になります。
情報基準では，一般的に対数尤度項とペナルティ項から成り立っています。
対数尤度にてモデルの精度を測定し，またペナルティを考慮することでモデルが過剰適合していないかということを組み込んで考えることができます。

LOOは対数尤度やペナルティの計算方法が異なっており，本記事においては両者とも計算してみました。
（コードを実行するだけなので，pythonで計算するのは簡単です！）

以下では，
　1.正規分布と仮定して作成したモデル
　2.スチューデントのt分布と仮定したモデル
を作成し，LOOによってどちらのモデルを選択すべきか考えてみます。

ライブラリとデータの読み込み

まずは，ライブラリとデータの読み込みを行います。

データには，scikit-learnのワインのデータセット（公式サイト）を使用しました。

#ライブラリのインポート
import pymc as pm
import arviz as az
from sklearn import datasets
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

#ワインデータの読み込み
data =  datasets.load_wine()
wine_data=data['data']
wine_target=data['target']
wine_X = pd.DataFrame(wine_data, columns=data['feature_names'])
df_wine = wine_X.copy()
df_wine['target']=wine_target
df_wine

ワインのデータセットの中身は以下のようになっています。

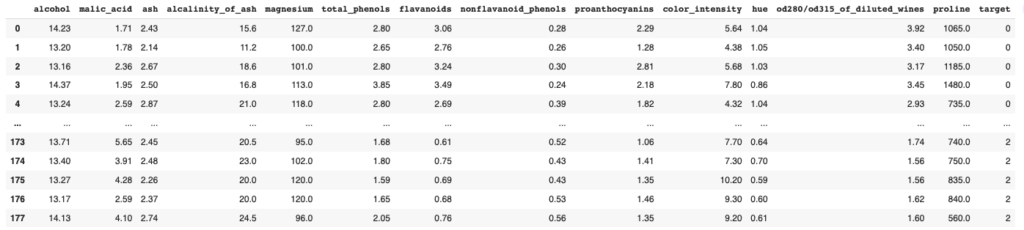
このデータセットは3種類のワインを調査したものであり，targetでそれぞの種類を0，1，2で表しています。
本記事では，target=0のalcalinity_of_ashの着目してその分布を推定しようと思います。

df_wine0= df_wine.query('target==0')
X = df_wine0['alcalinity_of_ash'].to_numpy()

X_mu = np.mean(X)
X_sd = np.std(X)
X_scaled = (X - X_mu) / X_sd

sns.histplot(X_scaled);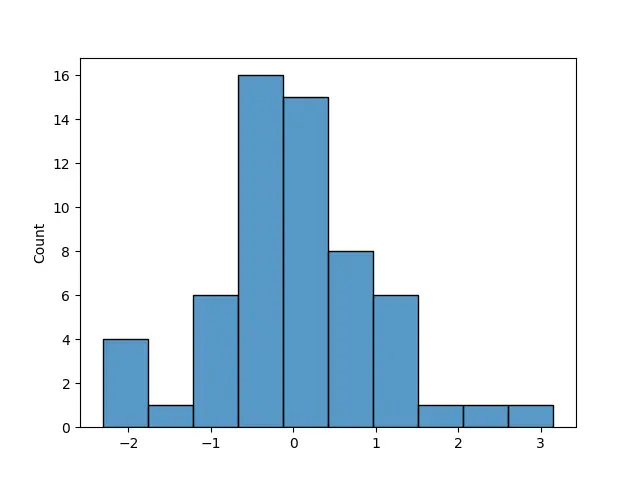

正規分布によるモデル作成

正規分布モデルの定義&サンプリング

まずは正規分布と仮定してモデルを作成していきます。

ここでは，正規分布のパラメータの事前分布を
　・平均値　　→ 一様分布
　・標準偏差　→ 半正規分布
としました（以下のコードの4,5行目）

model_n=pm.Model()

with model_n:
    mu = pm.Uniform('mu', -3, 3)
    sigma = pm.HalfNormal('sigma', sigma=10.0)
    X_obs = pm.Normal('X_obs', mu=mu, sigma=sigma, observed=X_scaled)

次にサンプリングを行います

with model_n:
    idata_n = pm.sample(chains=2,tune=2000,draws=2000, random_seed=42, return_inferencedata=True,idata_kwargs={"log_likelihood": True})

上記の通りWAICやLOOは，対数尤度で求めるので
idata_kwargs={"log_likelihood": True}
となっている点にご注意ください。

推論結果の確認

推論が正しく行えているか確認していきます。

az.plot_trace(idata_n, compact=False)
plt.tight_layout();

右側のグラフが2つとも一定の範囲でランダムノイズのようになっており，上手く推論できていることが確認できます，

summary_n=az.summary(idata_n)
display(summary_n)

さらに，r_hatも確認してみますが，こちらも1.01以下で上手く収束できていることが確認できました。

事後予測チェック

事後予測チェックを行います。

with model_n:
    idata_ppc = pm.sample_posterior_predictive(idata_n)

az.plot_ppc(idata_ppc, num_pp_samples=1000);

黒い線が実データ，青い線がベイズ推定で得られた結果になります。
黒い線が青い線の中に含まれているので，正しく推定できていそうということがわかります。

スチューデントのt分布

正規分布に従う現象は多くありますが，データに外れ値があると正規分布であっても上手く表現できないことがあります。
そのようなときに，外れ値を排除してしまうのが簡単にできる方法ですが，モデルを変更するという方法もあります。

スチューデントのt分布（Student’s t-distribution）は，正規分布と比較して両端が厚い分布になっています。つまり，平均値の周りに値が集中しすぎておらず平均から離れた値も表現しやすくなっています。

以下では，スチューデントのt分布は使ってモデリングをしたいと思います。

スチューデントのt分布モデルの定義&サンプリング

正規分布のとき同様に，モデルの定義とサンプリングから行なっていきます。

PyMCで設定するスチューデントのt分布のパラメータは，平均値( \mu\)，スケール( \sigma\)，自由度( \nu\)があり，今回，事前分布には，
平均値( \mu\)　→ 一様分布
スケール( \sigma\)　→ 半正規分布
自由度( \nu\)　→ 指数分布
としています。

model_t=pm.Model()

with model_t:
    mu = pm.Uniform('mu', -3, 3)
    sigma = pm.HalfNormal('sigma', sigma=10.0)
    nu = pm.Exponential('nu', 1/30)
    y = pm.StudentT('y', mu=mu, sigma=sigma, nu=nu, observed=X_scaled)

次は，サンプリングです。

with model_t:
    idata_t = pm.sample(chains=2,tune=2000,draws=2000, random_seed=42, return_inferencedata=True,idata_kwargs={"log_likelihood": True})

ここでも，idata_kwargs={"log_likelihood": True}となっている点にご注意ください。

推論結果の確認

続いて，推論結果の確認です。サクサクいきます。

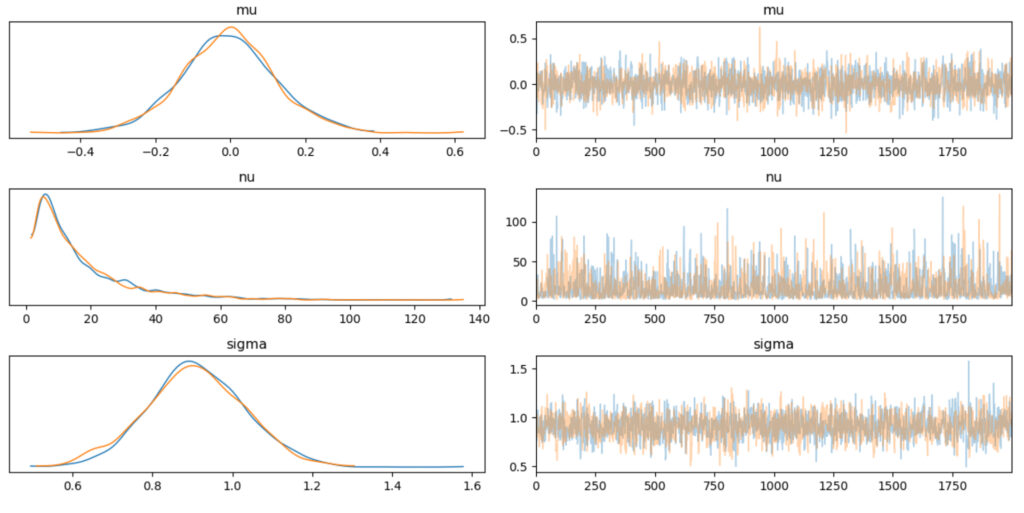
az.plot_trace(idata_t, compact=False)
plt.tight_layout();

正規分布のときと同様に問題なさそうです。

summary_t=az.summary(idata_t)
display(summary_t)

rhatも問題なさそうですね。

事後予測チェック

事後予測チェックです。

with model_t:
    idata_ppc_t = pm.sample_posterior_predictive(idata_t)

az.plot_ppc(idata_ppc_t, num_pp_samples=1000);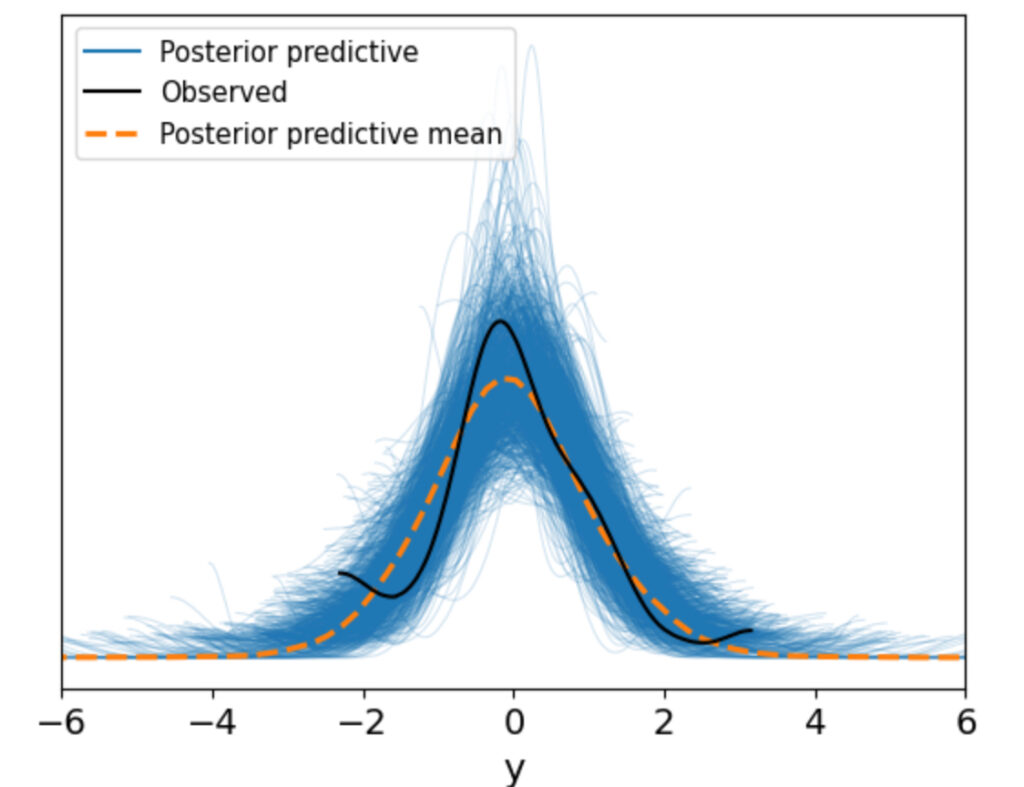

LOOによるモデル比較

ここまで長くなりましが，LOOを使い
　正規分布で作成したモデル
　スチューデントのt分布で作成したモデル
のどちらが良さそうか比較したいと思います，実行自体は数行できます！

dict_idata = {'Normal':idata_n, 'Studen-t':idata_t}
df_loo = az.compare(dict_idata, ic='loo', scale='deviance')
df_loo

まず，辞書型dict_idataに格納し、そしてaz.compareにて比較を行います。
結果としては↓下表です。
結果の表は，elupd_looが低い方が精度が良いモデルであり，elupd_looの低い順に表示されます。
したがってStudent-t分布の方が良いモデルということがわかります。

さらに，グラフ化もしてもます。

az.plot_compare(df_loo, figsize=(8, 3));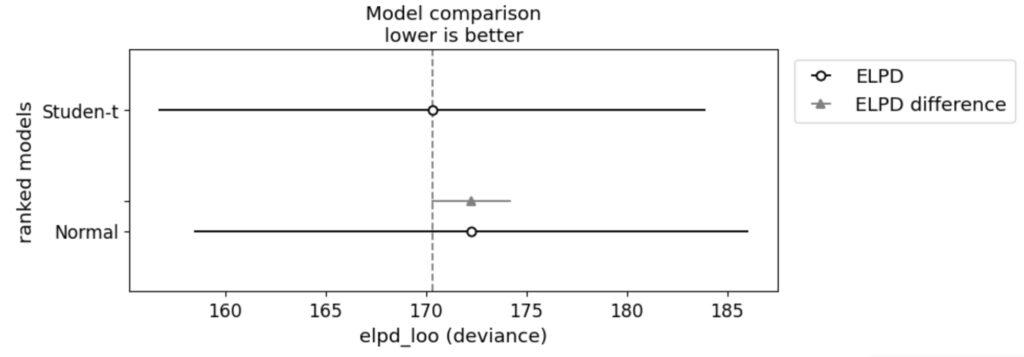

elupd_looをグラフ化したのものなので，結果は同じですがより視覚的に捉えることができます。