【ベイズ推論_PyMC5】正規分布によるモデリング

2024年7月31日2024年9月13日

ベイズ推論とは，データを確率モデルで表現する手法の一つです。

データをモデル化する最も有名な方法の1つに最尤推定がありますが，最尤推定では最も確からしいパラメータを点で求めるのに対して，ベイズ推定では，パラメータを点ではなく確率分布として求めることで幅として推定することができます。

本記事では，PyMCを用いてベイズ推論を行い，ベイズ推論への理解を深めたいと思います。
今回は，ワインのデータセットを用いて，正規分布へのベイズ推論を行います。

必要なライブラリとデータセットの読込み

まずは，ライブラリの読込みとデータセットの読み込みを行いたと思います。

#ライブラリのインポート
import pymc as pm
import arviz as az
from sklearn import datasets
import pandas as pd
import matplotlib.pyplot as plt

#ワインデータの読み込み
data =  datasets.load_wine()
X=data['data']
Y=data['target']
wine_X = pd.DataFrame(X, columns=data['feature_names'])
df_wine = wine_X.copy()
df_wine['target']=Y
df_wine

ワインのデータセットは3種類のワイン(target=0,1,2)に下図のような12の項目について調査したものになります。

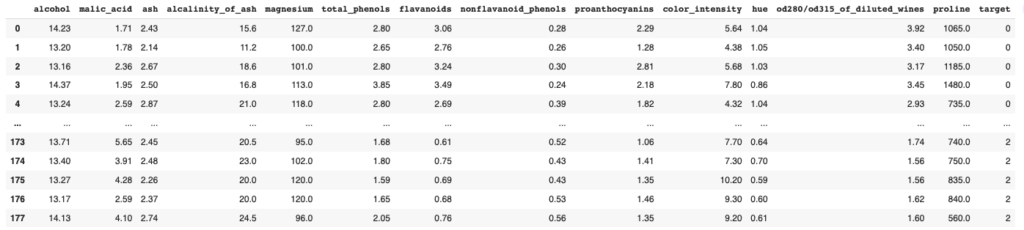
この12項目の中から今回はalcoholの項目，かつ3種類のwineの中からtarget=1のwineに注目して，モデルを作っていきたいと思います。

正規分布の確率モデルの定義

ここから，以下の4つのステップでベイス推論によるモデルの作成を行いたいと思います。

1.使用するデータの準備
2.モデルの定義
3.サンプリング
4.結果表示

1.は使うデータの準備です。
2,3.で実際のベイズ推論になります。ベイズ推論は，ベイズの定理である，

事後分布$ \propto$尤度×事前分布

に基づきます。
事後分布が今回推定したい確率分布であり，尤度は実測されたデータ，事前分布は事後分布の初期分布となります。

それでは1つ１つのステップを確認していきましょう。

STEP

使用するデータの準備

使用するデータは，前述の通りtarget=1でalcoholの項目とします。

下記にコードを示します。
1行目で.query()によりtarget=1を抜き出し後に、['alcohol']としてalcohol列のみを指定します。

抜き出したデータは，その後numpy配列に変換するため2行目で.to_numpyとしました。

コード1

df_wine1= df_wine.query('target==1')['alcohol']
X = df_wine1.to_numpy()

sns.histplot(X);

抜き出したデータを4行目でsns.histplot(X)でグラフ化しました。

STEP

モデルの定義

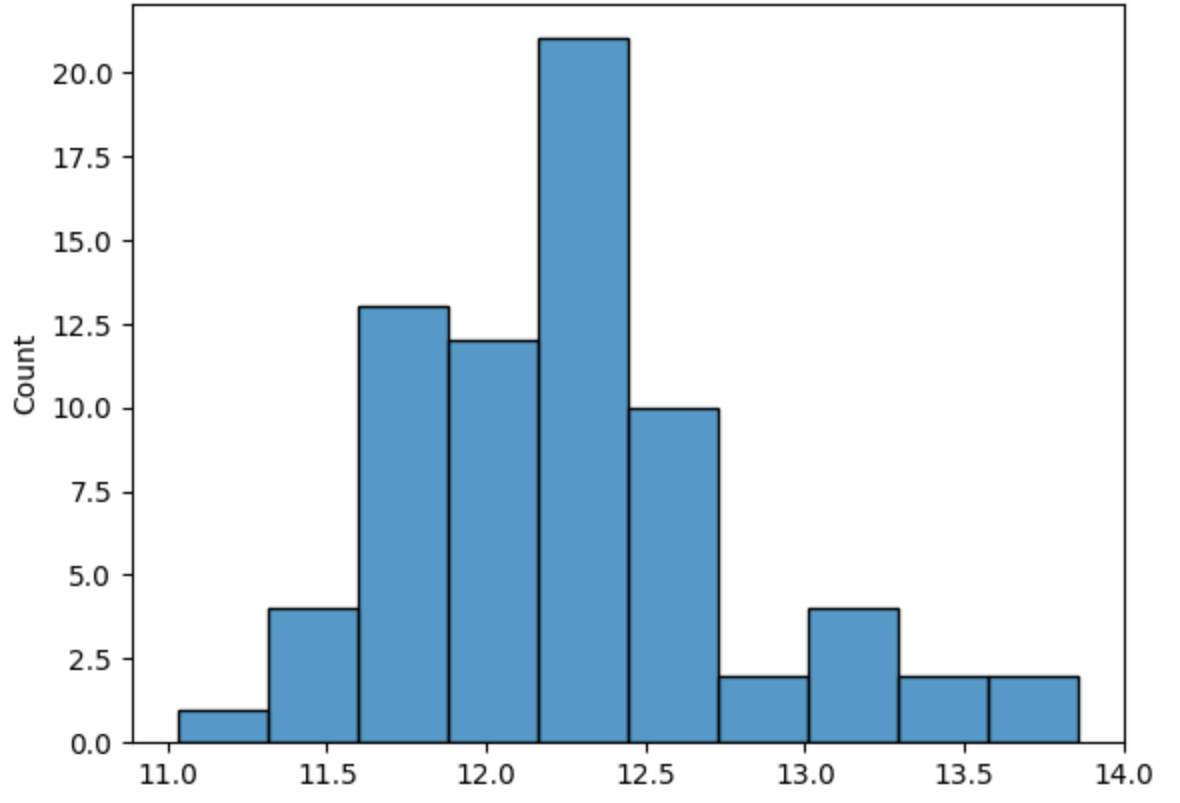
次は，モデルの定義を行います。

今回は正規分布に従うとして，ベイズ推論を行いたいと思います。
正規分布は，

$$f(x) = \frac{1}{\sqrt{2\pi} \sigma}\exp\left( – \frac{(x – \mu)^{2}}{2 \sigma^{2}}\right)$$

で表され，正規分布を決めるパラメータは平均 $ \mu$ と標準偏差 $ \sigma$ なので，この２つのパラメータの確率分布の推測を行っていきます。

ベイズ推論では，求めたい確率分布（今回は平均 $ \mu$と標準偏差 $ \sigma$）については，事前分布を決めておく必要があります。
今回は，平均 $ \mu$の事前分布を一様分布，標準偏差 $ \sigma$の事前分布を半正規分布としました。
このあたりは，求めたいパラメータが事前分布でカバーできていればオッケーです。

コードは以下のようになります。

コード2

model1=pm.Model()

with model1:
  mu = pm.Uniform('mu', 10, 15)
  sigma = pm.HalfNormal('sigma', sigma=10.0)
  X_obs = pm.Normal('X_obs', mu=mu, sigma=sigma, observed=X)

まず，1行目で今回作成するモデルのインスタンスを生成します。
これ以降，このmodel1にwith文で紐付ける形でモデルを作成していきます。

4行目では平均 $ \mu$ の事前分布を、5行目で標準偏差 $ \sigma$ の事前分布をそれぞれ定義しています。
それぞれの第一引数は、サンプリング時の結果解析で使用されるラベル名です。変数名とこのラベル名は慣例として同じものを使われることが多いので、それに倣いました。

コード2で確率モデルの定義ができたので、コード3でモデルの可視化も行なっておきます。

コード3

gv = pm.model_to_graphviz(model1)
display(gv)

gv.render(filename='model',format='png')

出力結果は下図のようになります。
これによって，確率変数間の関係が視覚的にわかるので是非作成してみてください。
コード3の3行目gv.render(filename='model',format='png')によって，png形式のmodelというファイル名で保存しています。

STEP

サンプリング

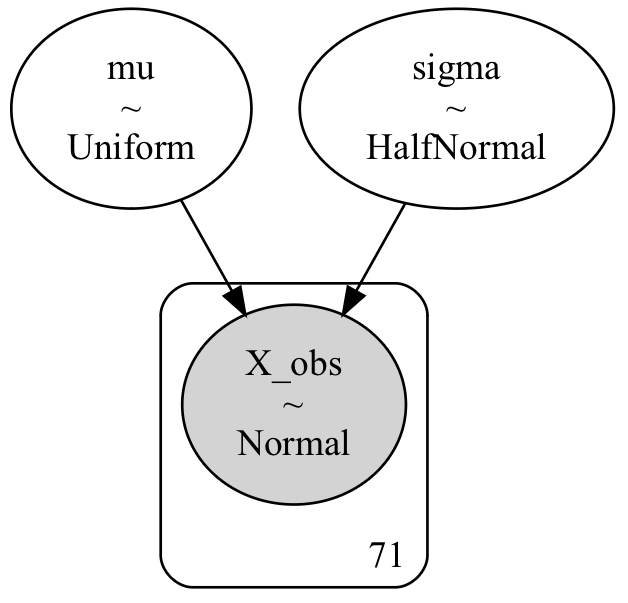
今回，事後分布$ \propto$尤度×事前分布　の事後分布を求めることが目的となりますが，事後分布を数学的に求めるのは複雑になることが往々にしてあります。
そこで，数学的な算出が複雑であっても，事後分布を擬した点列をサンプリングし事後分布を推定します。

ここではサンプリングを，MCMCという手法を用いて行います。

 with model1:
  trace1 = pm.sample(chains=2,tune=2000,draws=2000, random_seed=42, return_inferencedata=False)
  idata1 = pm.to_inference_data(trace1)

スクロールできます

chains	サンプル値系列
tune	取得するサンプル数
draws	捨てるサンプル数
random_seeds	シード値
return_inferencedata	FalseでMultiTrace、TrueでInferenceDataを返す。

return_inferencedataをFalseにすることで，MultiTraceで取り出しその後，pm.to_inference_data(trace1)でInferenceDataに変換しています。InferenceDataの方が詳しいサンプリングの情報を見ることができますが，MultiTraceの方が簡単にchainの本数やサンプリング結果を取り出せるので，今回は両方取得しています。

STEP

推論結果の確認

最後に，結果の確認をしていきます。

まずは，step3のサンプリング結果

az.plot_trace(idata1, compact=False)
plt.tight_layout();

結果は以下の通りです。

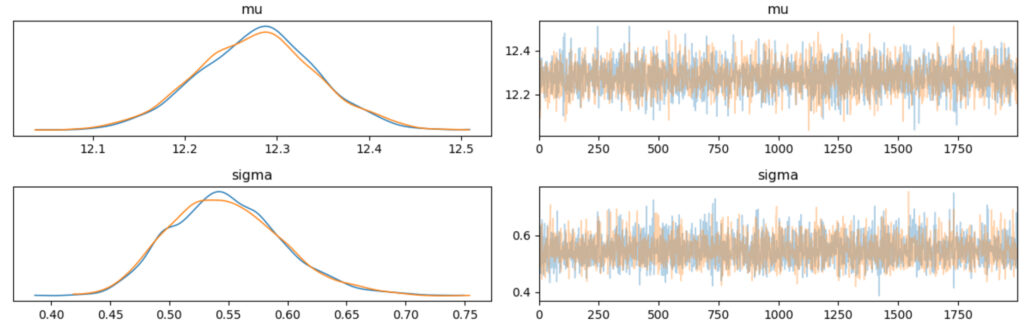
左側のグラフは縦軸に発生頻度，横軸が確率変数の値です。
mu, sigmaにそれぞれに2つの線がプロットされていますが，これはstep3でchains=2といているためであり，系列ごとにプロットしていることになります。結果の見方ですが，今回のように2つのプロットが同じ形を示していると上手く推論できていることを示しております。

右側のグラフは，縦軸が確率変数の値，横軸が繰り返し回数です。
繰り返し回数ですが，step3のdraws=2000と対応しており，グラフの最大値となっています。結果は，上図のように一定の範囲で何度も行き来していると正しくサンプリングできています。

次も推論が正しくできているかのチェック方法になります。

summary1=az.summary(idata1)
display(summary1)

mean, sd, hdi_3%, hdi_97%はサンプリング結果の統計量です。

その他の項目ですが，
　・mcse_mean：0.01以下
　・ess_bulk：400以上
　・r_hat：1.01以下
であれば，正しく推論できていることになります。

最後に，推論結果のmuとsigmaについてグラフ化してみます。

az.plot_posterior(idata1);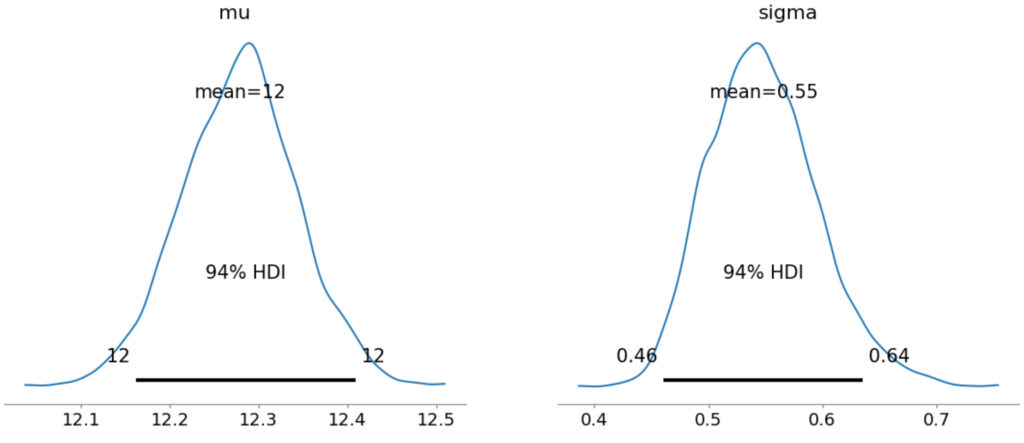

各グラフにある黒い線は，94%HDI (High density interval) の範囲です。

事後予測チェック

前章で，muやsigmaのパラメータの分布を得ることができました。
そこで，最後にこれらのパラメータの分布を使って，実際にどんなデータが得られるか確認してみようと思います。

with model1:

    ppc1 = pm.sample_posterior_predictive(idata1, return_inferencedata=False)
    idata_ppc1 = pm.to_inference_data(posterior_predictive=ppc1)

fig, ax = plt.subplots()
az.plot_ppc(idata_ppc1, ax=ax, num_pp_samples=1000)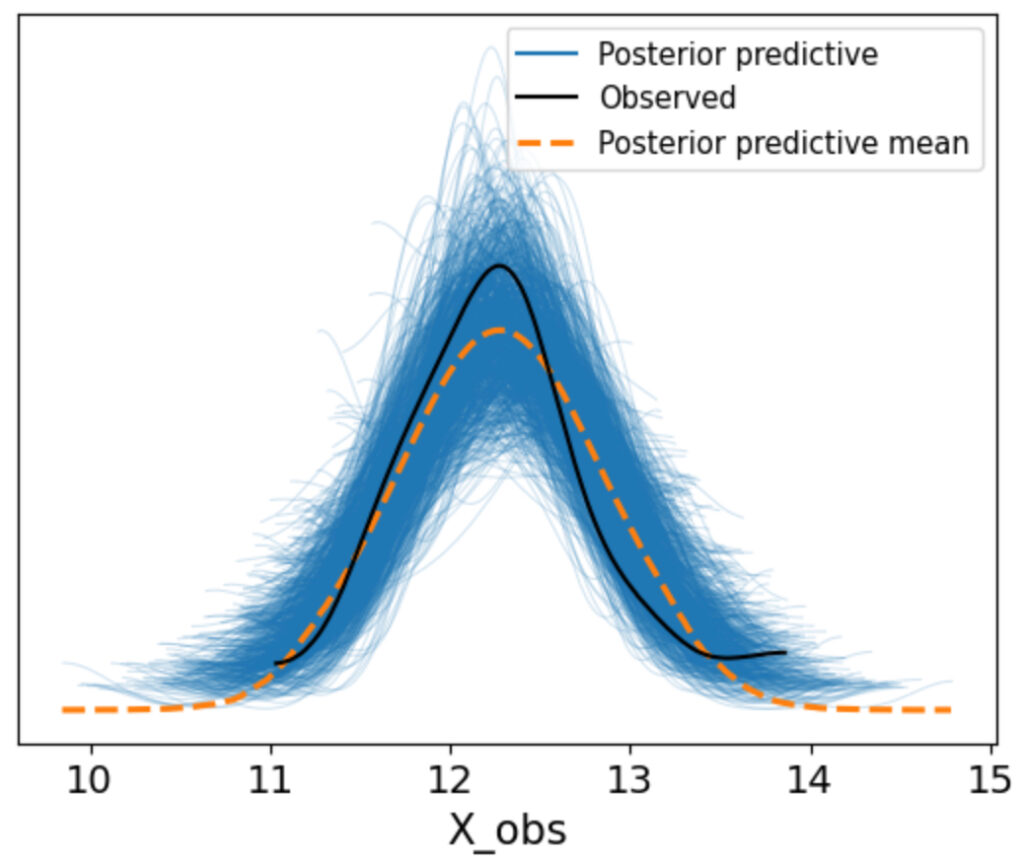

上図について，黒線が実際のデータ，青線が作ったモデルから推定したデータになります。今回，num_pp_samples=1000としているので1000本分の青線があります。
グラフを見てみると，実際のデータの黒線が青線の中に入っているので，正規分布で作成したモデルで正しく推定できそうということがわかりました。