この記事では,ベイズ推論を用いて線形回帰を行う方法を紹介します。
ベイズ推論で線形回帰を行うことで,最尤推定の1本の直線で表現されることと異なり,幅で表現することができます。
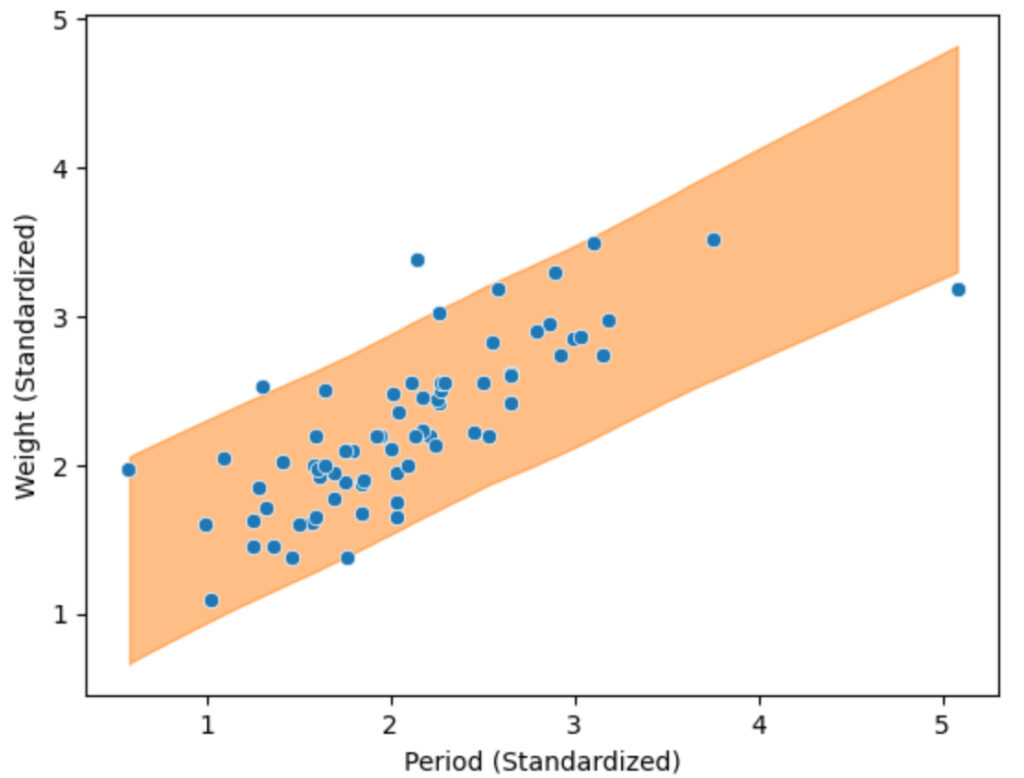
以下のようなグラフを作成することが目標になります。
ライブラリとデータセットの読み込み
まずは,ライブラリとデータセットの読み込みを行います。
#ライブラリのインポート
import pymc as pm
import arviz as az
from sklearn import datasets
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
#ワインデータの読み込み
data = datasets.load_wine()
X=data['data']
Y=data['target']
wine_X = pd.DataFrame(X, columns=data['feature_names'])
df_wine = wine_X.copy()
df_wine['target']=Y
df_winepymcはベイズ推論を行うために,arvizはpymcで生成したデータを可視化するために使用しています。
本記事では,以下のバージョンを使用しています。
print(pm.__version__)
# 5.10.4
print(az.__version__)
# 0.18.0また,データはsklearnからwineのデータセットを読み込んで使用しています。
データの中身は下図のようになっており,3種類のワイン(target=0,1,2)について,12項目の内容を調査した結果になります。
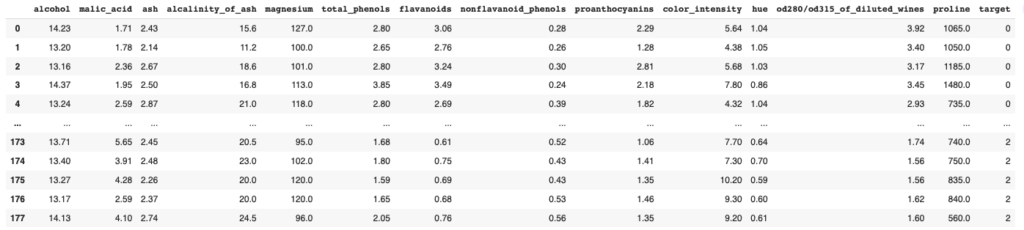
この12項目から,target=1のワインのflavanoidsとtotal_phenolsに注目して,ベイズ推論による線形回帰モデルを作成したいと思います。
ベイズ推論による線形回帰
target=1のワインのflavanoidsとtotal_phenolsに関して,以下の4つのステップでベイス推論による線形回帰を行なっていきます。
1.使用するデータの準備
2.モデルの定義
3.サンプリング
4.結果表示
1.は使うデータの準備です。
2,3.で実際のベイズ推論になります。ベイズ推論は,ベイズの定理である,
事後分布∝尤度×事前分布
に基づきます。
事後分布が今回推定したい確率分布であり,尤度は実測されたデータ,事前分布は事後分布の初期分布となります。
前述の通り,target=1のflavanoidsとtotal_phenolsのデータを使います。
コードは下記の通りです。
1行目で.query()を使いtarget=1を抜き出し,その後X, Yにそれぞれtarget=1のflavanoidsとtotal_phenolsを代入しました。
df_wine1 = df_wine.query('target==1')
X = df_wine1['flavanoids']
Y = df_wine1['total_phenols']
plt.scatter(X, Y);flavanoidsとtotal_phenolsの関係をグラフ化すると以下のようになります。
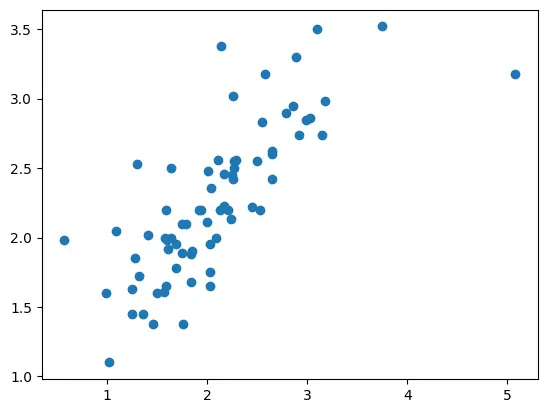
上図から,flavanoidsとtotal_phenolsは1次関数で近似できそうなので以下の式で表現しようと思います。
$$Y = \alpha X + \beta +\epsilon$$
ここで、 \( \epsilon\)は誤差にあたります。
最尤推定では, \( \alpha\)や \( \beta\)はただ一つのパラメータとして求めますが,ベイズ推定ではこれらのパラメータを確率分布として求めます。
上式を違う形で表現してみます。
$$ y \sim N(\mu =\alpha X + \beta, \sigma=\epsilon ) $$
この表現の方が,total_phenolsが平均値\( \alpha\)X + \( \beta\),標準偏差\( \epsilon\)とする正規分布に従うということがわかりやすいかもしれません。
先述の通り,
$$ y \sim N(\mu =\alpha X + \beta, \sigma=\epsilon ) $$
を表現するモデルを作成していきます。ここで繰り返しになりますが,yはtotal_phenols,xはflavanoidsになります。
コードは以下の通りです。
model1 = pm.Model()
with model1:
X_data = pm.ConstantData('X_data', X)
Y_data = pm.ConstantData('Y_data', Y)
alpha = pm.Normal('alpha', mu=0.0, sigma=10)
beta = pm.Normal('beta', mu=0.0, sigma=10)
mu = pm.Deterministic('mu', alpha * X_data + beta)
epsilon = pm.HalfNormal('epsilon', sigma=10)
Y_obs = pm.Normal('Y_obs', mu=mu, sigma=epsilon, observed=Y_data)説明が前後しますが,平均値を\( \alpha\)X + \( \beta\)とするため11行目で定義しています。
また,\(\alpha\)と\(\beta\)の事前分布をそれぞれ9,10行目で正規分布としました。
5,6行目のpm.ConstantDataですが,pymcで定数を表す表現となっており,X,YをそれぞれX_data, Y_dataと定義しています。
11行目のpm.Deterministicは,計算の途中でmuという確率変数を定義するための表現になります,
17行目において,誤差\( \epsilon\)の事前分布を半正規分布とし,19行目でYを平均\( \alpha\)X + \( \beta\),標準偏差\( \epsilon\)となるように定義しました。
ここまでで,定義したモデル構造を可視化してみます
コードは以下になります。
g = pm.model_to_graphviz(model1)
display(g)出力は下図のようになり,モデルの構造を可視化することができます。

モデルの定義ができたので,次はサンプリングを行います。
with model1:
trace1 = pm.sample(chains=2, tune=2000, draws=2000, random_seed=42, return_inferencedata=False)
idata1 = pm.to_inference_data(trace1)ここから推論が正しく行えているかをチェックしていきます。
チェックとしては3通りのやり方で確認していきます。
まずは以下のコードを実行してみます。
az.plot_trace(idata1, compact=False, var_names=['alpha', 'beta', 'epsilon'])
plt.tight_layout();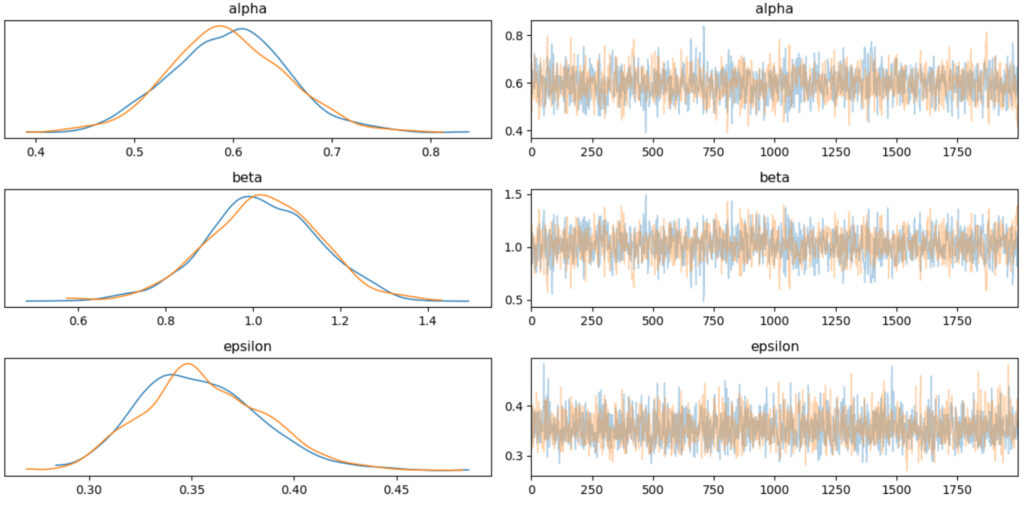
左側のグラフはalpha, beta, epsilonのパラメータがそれぞれプロットされています。
グラフの縦軸は発生頻度,横軸が確率変数の値です。
グラフ中にそれぞれに2つの線がプロットおり,これはstep3でchains=2といているためであり,系列ごとにプロットしていることになります。
グラフの見方ですが,2つのプロットが同じ形を示していると上手く推論できていることを示しています。
右側のグラフは,縦軸が確率変数の値,横軸が繰り返し回数です。繰り返し回数ですが,step3のdraws=2000と対応しています。
グラフは,一定の範囲で何度も行き来していると正しくサンプリングできています。
次は,統計量などからサンプリングが正しくできているか確認します。
summary1=az.summary(idata1, var_names=['alpha', 'beta', 'epsilon'])
display(summary1)上記のコードを実行すると以下の結果が得られます。

確認する項目としては,
・mcse_mean:0.01以下
・ess_bulk:400以上
・r_hat:1.01以下
であれば,正しく推論できている目安になります。
最後に,推論結果のmuとsigmaについてグラフ化してみます。
az.plot_posterior(idata1, var_names=['alpha', 'beta', 'epsilon']);結果は以下です。
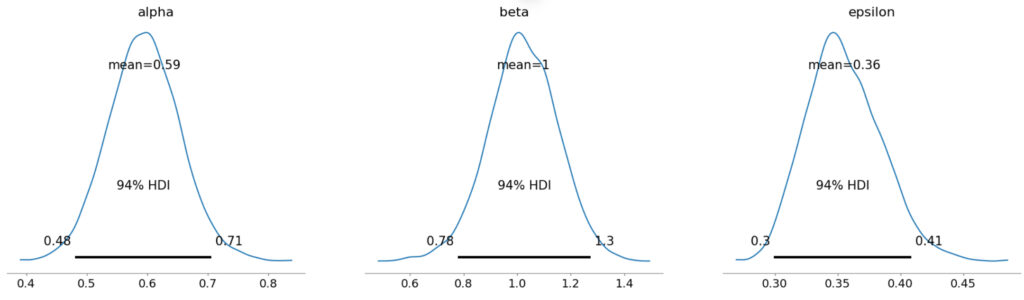
各グラフにある黒い線は,94%HDI (High density interval) の範囲です。
事後予測チェック
前章で,alpha, beta, epsilonのパラメータの分布を得ることができました。
そこで,最後にこれらのパラメータの分布を使って,実際にどんなデータが得られるか確認してみようと思います。
with model1:
ppc1 = pm.sample_posterior_predictive(idata1, return_inferencedata=False)
idata_ppc1 = pm.to_inference_data(posterior_predictive=ppc1)
az.plot_hdi(X, ppc1['Y_obs'])
sns.scatterplot(x=X, y=Y)#, hue=gender, s=80)
plt.xlabel('Period (Standardized)')
plt.ylabel('Weight (Standardized)');
上手において,帯となっている箇所が94%HDIとなっており,最尤推定の1本の直線で表現されることと異なり,幅で表現できることが確認できました。


コメント