【ベイズ推論_PyMC5】階層ベイズモデル

2024年9月20日

前回の記事では，1種類のwineのデータに対してベイズ推論により線形回帰モデルを扱いました。
本記事では，3種類のwineが混在しているデータに対してモデルを作成します。
モデルの作成にあたり階層ベイズモデルを用います。

階層ベイズでは，似た傾向のデータ同士を使うことで，データ数が少なくても推論を行うことが可能になります。
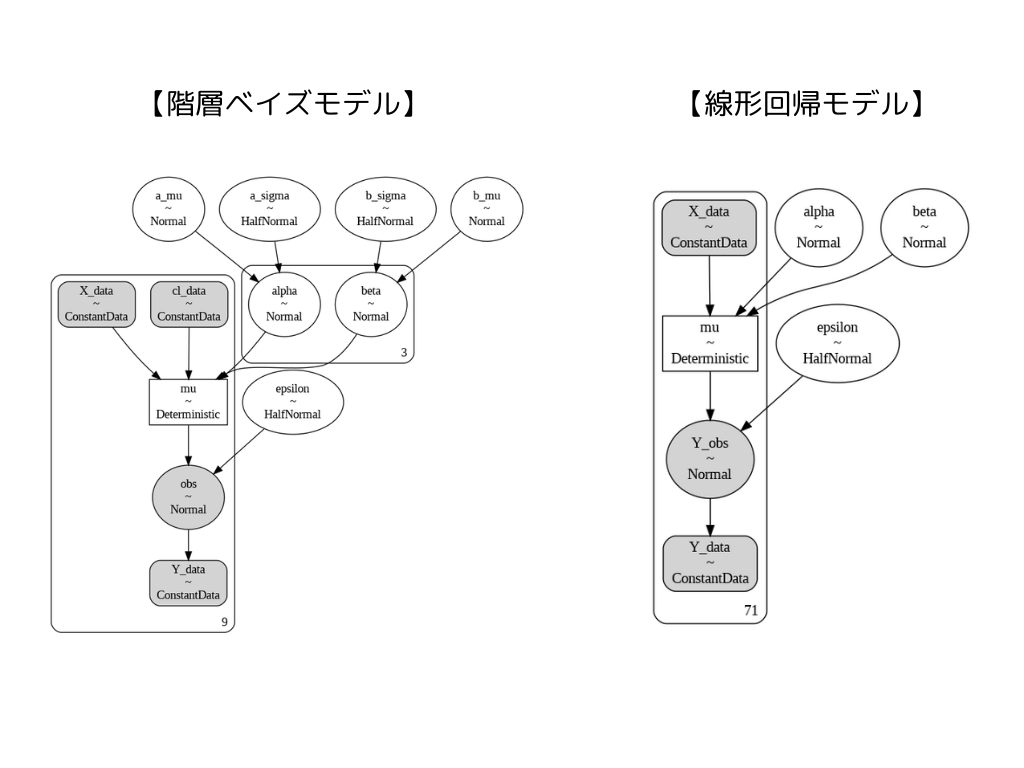
これは下図に示す通り，線形回帰モデルでは全てのデータに共通の事前分布として$ \alpha$や $ \beta$を扱っていましたが，階層ベイズモデルでは，その上にさらに事前分布を定義することで，”似た傾向のデータ”ごとの$ \alpha$や $ \beta$を表現できます。

ライブラリーとデータの読み込み

まず，ライブラリとデータの読み込みを行います。
データはscikit-learnのwineのデータセット（公式サイト）を使用しました。

#ライブラリのインポート
import pymc as pm
import arviz as az
from sklearn import datasets
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

#ワインデータの読み込み
data =  datasets.load_wine()
X=data['data']
Y=data['target']
wine_X = pd.DataFrame(X, columns=data['feature_names'])
df_wine = wine_X.copy()
df_wine['target']=Y
df_wine

このwineのデータセットの中からデータを抽出して，階層ベイズモデルを作成してみます。

df_wineの中身は以下のような13項目からなっています。
今回は，そのうちのflavanoidsと　color_intensityに着目して階層ベイズモデルを作成していきたいと思います。

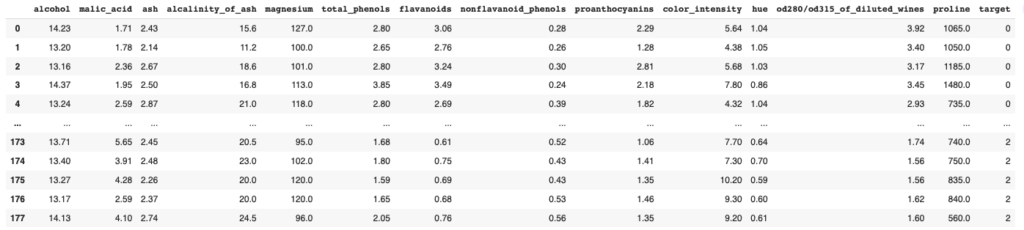
targetでワインの品種(0, 1,2)を示しています。
今回、階層ベイズモデルを試すため3品種について，それぞれn=3で抜き出しモデルの作成を行いたいと思います。

階層ベイズモデルの作成

ここから階層ベイズモデルを以下の４つのstepで作成していきます。

データの準備
モデルの定義
サンプリング
推論結果の確認

以下，それぞれのstepで準備していきます。

STEP

データの準備

前述の通り，df_wineからそれぞれのwineの品種ごとにflavanoidsと　color_intensityを準備します。
1〜3行目で品種ごとにデータを抜き出し，5〜7行目で3サンプルだけ抜き出します。
その後、11,12行目でflavanoidsと　color_intensityを取り出します。

df_wine0 = df_wine.query('target==0')
df_wine1 = df_wine.query('target==1')
df_wine2 = df_wine.query('target==2')

df_wine0_sel = df_wine0.sample(n=3, random_state=42)
df_wine1_sel = df_wine1.sample(n=3, random_state=42)
df_wine2_sel = df_wine2.sample(n=3, random_state=42)

df_wine_sel = pd.concat([df_wine0_sel, df_wine1_sel, df_wine2_sel,])

X = df_wine_sel['flavanoids'].values
Y = df_wine_sel['color_intensity'].values
target = df_wine_sel['target']
cl = pd.Categorical(target).codes

clは抜き出した3サンプルが，どの品種にグループに属するかを示すインデックスが格納されています。

また，抜き出したサンプルを描画すると下図のようになります。

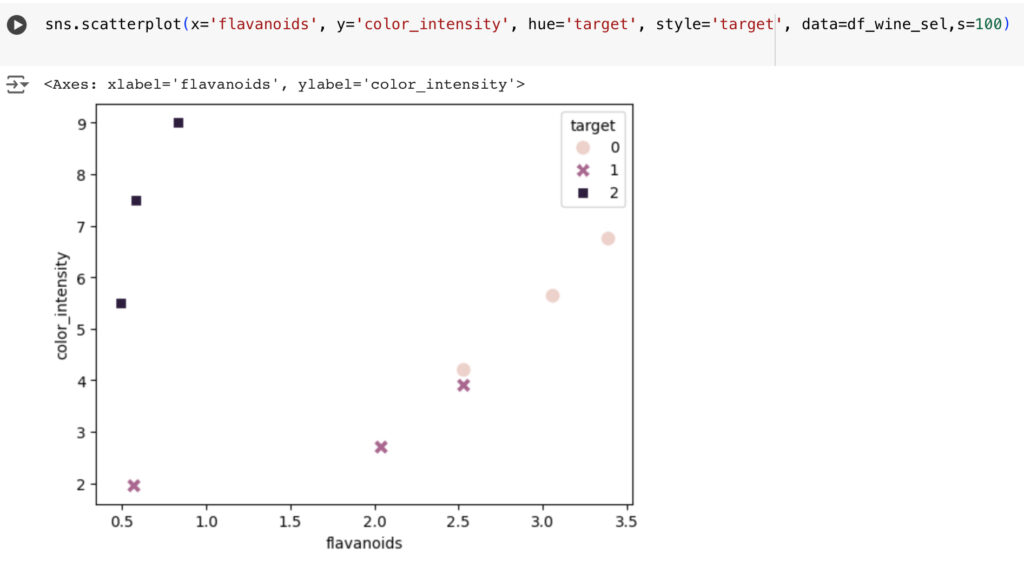
今回はこのflavanoidsと　color_intensityの関係を，

$$Y = \alpha X + \beta +\epsilon$$

という数式で表現します。
ここで、 $ Y$はcolor_intensity，$ X$はflavanoids，$ \epsilon$が誤差にあたります。
階層ベイズモデルでは， $ \alpha$や $ \beta$の上にさらに事前分布を定義し品種違いであっても1つのモデルで定義します。

STEP

モデルの定義

ここから実際のモデルの定義を行います。

model1 = pm.Model()

with model1:
  X_data = pm.ConstantData('X_data', X)
  Y_data = pm.ConstantData('Y_data', Y)
  cl_data = pm.ConstantData('cl_data', cl)

  a_mu = pm.Normal('a_mu', mu=0.0, sigma=10.0)
  a_sigma = pm.HalfNormal('a_sigma', sigma=10.0)
  alpha = pm.Normal('alpha', mu=a_mu, sigma=a_sigma, shape=(3,))

  b_mu = pm.Normal('b_mu', mu=0.0, sigma=10)
  b_sigma = pm.HalfNormal('b_sigma', sigma=10.0)
  beta = pm.Normal('beta', mu=b_mu, sigma=b_sigma, shape=(3,))

  epsilon = pm.HalfNormal('epsilon', sigma=1.0)

  mu = pm.Deterministic('mu', X_data*alpha[cl_data]+beta[cl_data])

  obs = pm.Normal('obs', mu=mu, sigma=epsilon, observed=Y_data)

4-6行目で，X_data, Y_dataとcl_dataについてpm.ConstantDataを使い定数として定義しています。
その後，8-16行目で各確率変数の定義を行っています。
このたあたりの関係についてはモデル構造の可視化を行うと理解しやすくなります。
可視化については，下記のコードを実行します。

線形回帰モデルなどのときとは異なり， $ \alpha$や $ \beta$はwineの品種によって異なることを表すため，$ \alpha$や $ \beta$の上位に事前分布が定義されていることが確認できます。

g = pm.model_to_graphviz(model1)
display(g)

STEP

サンプリング

ここではサンプリングを行います。

with model1:
  idata1 = pm.sample(random_seed=42,tune=2000,draws=2000, target_accept=0.998)

STEP

推論結果の確認

推論結果の確認をしていきます。

まずplot_trace関数を使い推論結果を確認です。
ver_nameで確認する変数を指定することができ，今回$ \alpha$や $ \beta$を指定しています。

az.plot_trace(idata1, compact=False, var_names=['alpha', 'beta'])
plt.tight_layout();

上記のグラフから，2つのサンプル値系列で同じ傾向を示しており問題なく推論できていることが確認できます。

次は，summary関数を使った確認です。

summary1 = az.summary(idata1, var_names=['alpha', 'beta'])
display(summary1)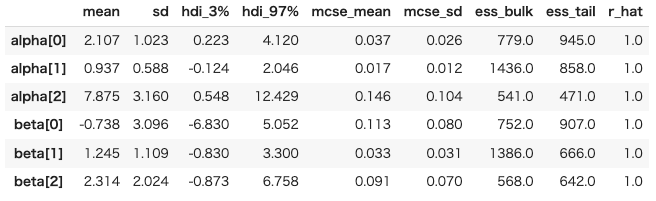

ここで，r_hatが1.01以下であるため正しく推論できていそうということが確認できます。

推論値と実測値の比較

前章で推論した結果をもとに，回帰直線を描画し実測値とどの程度あっているか可視化してみようと思います。

means = summary1 ['mean']
alpha0 = means['alpha[0]']
alpha1 = means['alpha[1]']
alpha2 = means['alpha[2]']
beta0 = means['beta[0]']
beta1 = means['beta[1]']
beta2 = means['beta[2]']

x_range = np.arange(0.4, 3.6)
pred_wine0 = alpha0 * x_range + beta0
pred_wine1 = alpha1 * x_range + beta1
pred_wine2 = alpha2 * x_range + beta2

sns.scatterplot(x='flavanoids', y='color_intensity', hue='target', style='target', data=df_wine_sel,s=100)
plt.plot(x_range, pred_wine0, label='pred_0')
plt.plot(x_range, pred_wine1, label='pred_1')
plt.plot(x_range, pred_wine2, label='pred_2')
plt.legend();

結果は以下の通りです。概ね正しそうな傾向を示しています。

上図のグラフは，全体から3つずつ抜き出した結果なので，全体のデータと今回推論した値の傾向を比較してみます。

x_range = np.arange(0.4, 6)
pred_wine0 = alpha0 * x_range + beta0
pred_wine1 = alpha1 * x_range + beta1
pred_wine2 = alpha2 * x_range + beta2

plt.plot(x_range, pred_wine0, label='pred_0')
plt.plot(x_range, pred_wine1, label='pred_1')
plt.plot(x_range, pred_wine2, label='pred_2')

sns.scatterplot(x='flavanoids', y='color_intensity', hue='target', style='target', data=df_wine,s=100)
plt.legend();